Appassionato elogio di chi sbaglia Col contributo di cantonate illustri

Se Shimura era meticoloso, Taniyama era trascurato fino all’indolenza. Sorprendentemente Shimura ammirava questo suo tratto: «Lui era dotato della capacità speciale di fare molti errori, per lo più nella direzione giusta. Lo invidiavo per questo, e tentavo di imitarlo, ma mi era molto difficile fare buoni errori». Così sono presentati da Simon Singh i due ragazzi giapponesi autori di una famosa congettura matematica che porta il loro nome e che ha contribuito alla soluzione di un ancor più famoso caso matematico noto come “ultimo teorema di Fermat”. Parafrasando Oscar Wilde, per fare buoni errori ci vuole talento, ma riconoscere che si tratta di una virtù è proprio solo del genio.

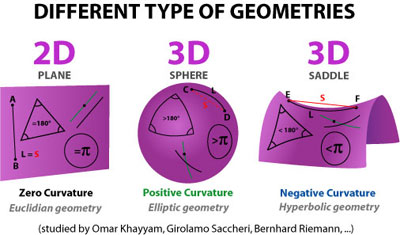
Uno degli errori più belli della storia. Lo commise il gesuita e matematico Giovanni Girolamo Saccheri quando scoprì che esistevano dei quadrilateri con la somma degli angoli interni (rigorosamente fissata da Euclide in 360 gradi; pensate a un rettangolo) più grande del limite indicato dal geometra greco. Il Saccheri si prese un tale spavento di fronte al risultato che lui stesso aveva prodotto (per la matematica dell’epoca era come aver scoperto che certe gocce d’acqua salgono, invece di scendere) da rivedere la dimostrazione, trovarci un errore che non c’era, e lasciar stare il mondo com’era sempre andato. Ci volle più di un secolo perché qualcun altro avesse il coraggio di dichiarare che il vecchio gesuita sanremese aveva avuto tutte le ragioni per pensare quello che aveva pensato; gli sarebbe bastato immaginare che, accanto alla tradizionale geometria euclidea, ne esistesse un’altra altrettanto rigorosa: quella che fu poi detta curva e che risultò molto utile - fra gli altri - ad Albert Einstein. L’errore di Saccheri consistette nel credere di aver commesso un errore e nell’aver - successivamente - voluto sbagliare di proposito per poter dire a se stesso di essersi sbagliato. Come contorcimento mentale non c’è malaccio.

[Richard Feynman]

Qualche clausola per errori “buoni” (e un esempio). Gli errori, però, non sono tutti uguali e, soprattutto, per essere “buoni” devono cadere in un terreno fertile. Altrimenti passano inosservati. Dagli sbagli, infatti, impara solo chi sta cercando qualcosa di molto preciso: solo chi sta andando in una certa direzione può infatti misurare la distanza che separa l’obiettivo previsto dal risultato ottenuto e valutare la qualità della differenza. Solo chi è certo (almeno in ipotesi) di come le cose dovrebbero andare può mettersi a cercare il motivo per cui qualcosa “non ha funzionato”, o la ragione per cui certi conti “non sono tornati”.

James Gleick, il grande divulgatore scientifico americano, racconta a questo proposito una bella storia nell’Introduzione a “Genio”, una biografia di Richard Feynman, uno dei più grandi matematici e fisici del nostro tempo. Parla degli scienziati che, dopo aver condotto a termine l’esperimento che avrebbe poi portato alle bombe di Hiroshima e Nagasaki, capirono abbastanza presto quanto fragile fosse la loro teoria: «Avevano pensato che la meccanica quantistica offrisse un modo preciso, forse provvisorio, ma almeno funzionale, di fare calcoli sulla luce e la materia. Una volta portata alle sue estreme conseguenze, tuttavia, la teoria aveva prodotto risultati errati. Più che errati, semplicemente insensati». Come dire che la bomba era scoppiata, ma per ragioni che non c’entravano nulla (o quasi) con quelle che loro, i progettisti, avevano immaginato. Una cosa sola rimaneva certa: che i giapponesi non erano in grado di capire dove stesse l’errore. E non perché erano morti, ma perché una “cosa” come quella non rientrava nel loro orizzonte mentale.

La lezione dello Lo scarabeo d’oro. I giapponesi non potevano capire perché non si trovavano nelle condizioni in cui è collocato - dal suo autore - uno dei protagonisti del racconto che più di ogni altro spiega come si producano - e si correggano - gli errori: Lo scarabeo d’oro, di Edgar A. Poe. William Legrand - il soggetto in questione - sta spiegando al suo amico e scettico interlocutore - il narratore - come abbia fatto a metter le mani su un immenso tesoro. Un passo della “caccia” consisteva nel calare un filo a piombo attraverso l’occhio destro di un teschio inchiodato sul ramo di albero. Prolungata di un certo numero di volte la linea che andava dalla base dell’albero al punto ricavato sul terreno in questo strano modo, e dato mano al piccone, si sarebbe trovata la cassa coi dobloni. Ma quando Legrand, seguite tutte le indicazioni, si mette a scavare, la cassa non si fa trovare. A questo punto ha l’intuizione geniale: l’occhio destro del teschio era, in realtà, il sinistro per l’osservatore. Rifatta l’operazione da capo, cioè calato il filo attraverso l’orbita giusta, la distanza iniziale tra i due punti d’impatto sul terreno risultava di pochi centimetri ma, col prolungarsi della semiretta (ossia del lato dell’angolo), il primo e il secondo luogo in cui effettuare lo scavo distavano fra loro diversi metri. E questa seconda volta, in effetti, il baule venne fuori.

Cosa vorrebbe dimostrare questa storia. Diverse cose. La prima è che un lungo processo dimostrativo può portare a una delusione anche a causa di un piccolo errore di percorso. Il personaggio del racconto aveva capito perfettamente come doveva procedere per poter entrare in possesso del tesoro, ma rischiava di dover dire a se stesso di aver lavorato invano - e di essere deriso dal suo amico che lo credeva matto - solo a causa di una svista procedurale. Errori di questo tipo non portano a niente e, anzi, è meglio evitarli.

La seconda è che bisogna essere molto convinti di aver ragione per decidere di tornare a controllare un procedimento che si è concluso in maniera infelice. Per poter verificare un’ipotesi - ha detto un grande matematico - bisogna sapere da molto prima che essa è vera e agire come se lo fosse, altrimenti non si va da nessuna parte.

La terza è che Poe sa che è impagabile la condizione di chi può accorgersi di avere sbagliato, perché questo lo certifica ancor più sulla correttezza della propria intuizione.

Un esempio che ha fatto la storia. Ad esempio, Cristoforo Colombo si sbagliò di grosso circa l’ampiezza in longitudine dell’oceano che separava la Spagna dalle Indie. Si sbagliò anche nell’immaginare che fra i domini del Re Cattolico e la terra dei Marajah non esistesse una qualunque terra emersa. Ma quel che nacque da questo doppio errore fu la consapevolezza provata della correttezza della sua teoria.

Certo: Colombo fu fortunato a sbattere contro le isole caraibiche perché in loro assenza lui e tre equipaggi sarebbero morti di fame e di sete in mezzo al mare. La teoria, si vuol dire, per poter essere verificata ha bisogno che in suo soccorso si mobiliti una quantità di eventi casuali da far paura. Per esempio, che l’America sia a una distanza dall’Europa tale da consentire che le scorte di acqua e cibo a bordo non si esauriscano, che le terrificanti bonacce equatoriali ad un certo punto la smettano di fare le bonacce e decidano di lasciare il passo a qualche corrente d’aria.

Per questo si dice che per poter sbagliare con profitto bisogna commettere errori che non implichino la morte dello sperimentatore. O che almeno un suo parente prossimo o allievo diletto e fortunato sopravviva al botto fatale.